It was a nice game but it did not really last for as long as I had hoped for.
]]>curl -fsSL https://opencode.ai/install | bash
opencode --version
Config lives in ~/.config/opencode/.
Fire up LM Studio and load a code-focused model – something like Qwen3 Coder 30B works well if your hardware can handle it. Make sure the local server is running, by default it listens on http://localhost:1234.
Then edit ~/.config/opencode/opencode.json:
{
"$schema": "https://opencode.ai/config.json",
"provider": {
"lmstudio": {
"npm": "@ai-sdk/openai-compatible",
"name": "LM Studio (local)",
"options": {
"baseURL": "http://localhost:1234/v1"
},
"models": {
"zai-org/glm-4.7-flash": {
"name": "glm-4.7-flash"
}
}
}
}
}
The key bit is @ai-sdk/openai-compatible – LM Studio exposes an OpenAI-compatible API, so this just works.
Launch opencode and run /model to verify. You should see “LM Studio (local)” as an available provider.
The nice thing about running everything locally is that your code never leaves your machine, there are no token limits, no API costs, and it works offline. The tradeoff is output quality – local models are getting better fast but still lag behind frontier cloud models for complex reasoning. For code review, refactoring suggestions, and boilerplate generation though, they work surprisingly well.
]]>concise commandline monitoring for containers
numel and element_size:
import torch
def get_size(t: torch.Tensor):
return t.numel() * t.element_size()
That’s it!
]]>
It was a nice game but it did not really last for as long as I had hoped for.
]]>You can, just add .atom to the original URL of the Gist profile and et voilà!
More verbosely, subscribe to https://gist.github.com/{username}.atom from your feed reader of choice.
Firecracker is an open source virtualization technology that is purpose-built for creating and managing secure, multi-tenant container and function-based services.
Firecracker enables you to deploy workloads in lightweight virtual machines, called microVMs, which provide enhanced security and workload isolation over traditional VMs, while enabling the speed and resource efficiency of containers.
Firecracker is a virtual machine monitor (VMM) that uses the Linux Kernel-based Virtual Machine (KVM) to create and manage microVMs.
Firecracker is generally available on 64-bit Intel, AMD and Arm CPUs with support for hardware virtualization. 🤯
Julia Evans has a fantastic post on the same: Firecracker: start a VM in less than a second, you should give it a read!
]]>V8 orchestrates isolates: lightweight contexts that provide your code with variables it can access and a safe environment to be executed within. You could even consider an isolate a sandbox for your function to run in.
A single instance of the runtime can run hundreds or thousands of isolates, seamlessly switching between them. Each isolate’s memory is completely isolated, so each piece of code is protected from other untrusted or user-written code on the runtime. Isolates are also designed to start very quickly. Instead of creating a virtual machine for each function, an isolate is created within an existing environment. This model eliminates the cold starts of the virtual machine model.
That reads suspiciously like threads, doesn’t it? Yes, sort of – it depends on the implementation. This is what Chromium’s Blink has to say:
An isolate is a concept of an instance in V8. In Blink, isolates and threads are in 1:1 relationship. One isolate is associated with the main thread. One isolate is associated with one worker thread.
Anyway, circling back to what Cloudflare workers – I wonder what the implications for security and isolation are across the various isolates? There’s various threads of discussion on this, notably this thread from the orange website. It defers the decision to it depends with process based isolation being preferred when running untrusted code.
]]>
Yep, that’s right – there’s CSS in that Atom feed, turns out you can do it.
Here’s another blog posting describing how: https://andrewstiefel.com/style-atom-xsl/.
And now its in action here: https://blog.sayan.page/feed.xml, that’s all!
]]>docker exec -it immich_postgres bash
psql immich postgres
immich=# select email,"isAdmin" from users;
UPDATE users SET "isAdmin"='t' WHERE email='email@example.com';
And that’s it!
]]>mitmproxy server
Install the mitmproxy server on your platform of choice.
The instructions on mitmproxy.org are fairly straightforward to follow!
After installing, run the mitmproxy command to start the proxy server.
Note the IP address/hostname (let’s call this proxyhost) of the computer that is running the proxy server, by default the server listens on port 8080.
Essentially, we should have the proxy server reachable at proxyhost:8080 now for any device on the same network as the proxy server.
Head over to Settings > WiFi and then tap on the (i) icon beside the network your are connected to.
See: Screenshot 0
Scroll down to the bottom of the page and then tap on the option that says “Configure Proxy”.
See: Screenshot 1
Use the proxy server IP and port from earlier (proxyhost:8080) and hit save.
See: Screenshot 2
Open Safar on the iOS device and head over to mitm.it. You will be greeted with a page that lists CA certificates for various platforms, tap on the one that is for iOS.
See: Screenshot 3
Tap on allow to download mitmproxy’s CA cert to the iOS device’s certificate store.
See: Screenshot 4
Choose the device that you want to install the CA certificate too. Most likely you would want to choose the iPhone from the list.
See: Screenshot 5
The CA certificate for mitmproxy is now downloaded, we need to head on over to the Settings apps now.
See: Screenshot 6
When you open the Settings app on iOS device, you’ll be greeted with a list item titled “Profile Downloaded”. Tap on that!
See: Screenshot 7
Then tap on the “Install” button on the top right corner.
See: Screenshot 8
After that head on to Settings > General > About and scroll down to the bottom of the page.
You will see a menu item titled “Certificate Trust Settings”.
Tap on it, in the following page enable the certifcate for mitmproxy.
See: Screenshot 9
That’s it, you will now be able to intercept SSL traffic from your iOS device on the proxy server.
I would recommend disabling or removing the mitmproxy CA certificate when not in use, you can simply toggle it in Settings > General > About > Certificate Trust Settings.
You would also need to disable the proxy server configuration for the network whenever you turn off the proxy server. You can do that by heading over to Settings > WiFi and then tap on the (i) icon beside the network your are connected to. Scroll down to the bottom of the page and then tap on the option that says “Configure Proxy” and then tap on the “Off” option from the list.
You will not be able to interecept SSL traffic for any application that uses certificate pinning. This is because these applications bypass the system certificate store and have their own trust store for certificates. See https://docs.mitmproxy.org/stable/concepts-certificates/#certificate-pinning on working around certificate pinning.
]]>This is where companies like Markmonitor come into the picture. Their services include:
software intended to protect corporate brands from Internet counterfeiting, fraud, piracy, and cybersquatting
Markmonitor has an impressive clientele involving the likes of companies such as Amazon, Google, Akamai, Alibaba, Baidu etc!
Essentially, think of Markmonitor as a service that reminds you to pay for your domain names before they expire so that you aren’t bullied into someone on the interwebs squatting your domain name. This is quite amusing to me as an individual but it is a sensible service nonetheless that benefits corporations.
I still find it quite hard to wrap my head around this. :)
# whois.markmonitor.com
Domain Name: amazon.com
Registry Domain ID: 281209_DOMAIN_COM-VRSN
Registrar WHOIS Server: whois.markmonitor.com
Registrar URL: http://www.markmonitor.com
Updated Date: 2023-05-16T18:56:31+0000
Creation Date: 1994-11-01T05:00:00+0000
Registrar Registration Expiration Date: 2024-10-30T07:00:00+0000
Registrar: MarkMonitor, Inc.
# whois.markmonitor.com
Domain Name: akamai.com
Registry Domain ID: 2906556_DOMAIN_COM-VRSN
Registrar WHOIS Server: whois.markmonitor.com
Registrar URL: http://www.markmonitor.com
Updated Date: 2022-04-11T18:10:46+0000
Creation Date: 1998-08-17T04:00:00+0000
Registrar Registration Expiration Date: 2024-08-16T04:00:00+0000
Registrar: MarkMonitor, Inc.
# whois.markmonitor.com
Domain Name: google.com
Registry Domain ID: 2138514_DOMAIN_COM-VRSN
Registrar WHOIS Server: whois.markmonitor.com
Registrar URL: http://www.markmonitor.com
Updated Date: 2019-09-09T15:39:04+0000
Creation Date: 1997-09-15T07:00:00+0000
Registrar Registration Expiration Date: 2028-09-13T07:00:00+0000
Registrar: MarkMonitor, Inc.
tar is a cryptic mess and everytime you need to use it you need to head back to the man page to look them up?
Well fear no more – you could just remember these mnemonic flags instead and make your life easier!
$ file archive.tar.gz
archive.tar.gz: gzip compressed data, last modified: Sun Dec 24 13:42:15 2023, from Unix, original size modulo 2^32 1372672
Use wtf: what the fuck is in that archive?
$ tar wtf archive.tar.gz
- 8<-
Use pfx: please fucking extract the archive!
$ tar pfx archive.tar.gz
- 8<-
MacOS: Ctrl + Shift + Option + Q
Windows: Ctrl + Shift + Alt + Q
This will bring up an overlay dialog with wide range of statistics and debugging information.
Note: This shortcut does not work when you are in fullscreen mode.
]]>__debug__ constantPython has a built-in boolean constant
named __debug__.
It is set to True whenever you run a REPL shell or call a script with the
python script.py i.e. by default.
It is set to False only when you pass the -O or the -OO flags to the python executable.
These flags are described in the Python manual page as:
-O Remove assert statements and any code conditional on the value of debug;
augment the filename for compiled (bytecode) files by adding .opt-1 before the .pyc
extension.
-OO Do -O and also discard docstrings; change the filename for compiled
(bytecode) files by adding .opt-2 before the .pyc extension.
__debug__ in REPL shell$ python3
Python 3.9.13 (main, May 24 2022, 21:28:31)
[Clang 13.1.6 (clang-1316.0.21.2)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> __debug__
True
$ python3 -O
Python 3.9.13 (main, May 24 2022, 21:28:31)
[Clang 13.1.6 (clang-1316.0.21.2)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> __debug__
False
__debug__ in scripts$ cat script.py
print(__debug__)
$ python3 script.py
True
$ python3 -O script.py
False
$ python3 -OO script.py
False
The domain name system (DNS), for the lack of a better analogy, is similar to the concept of phone books. You know the name of the person you want to reach but you don’t know their phone number – so you look it up in the phone book and connect to them.
Unlike phone numbers that we humans use to communicate, computers communicate with each other via IP addresses.
When you want to visit a website – say instagram.com – your computer does not know where that is. So, your computer queries the DNS servers on the internet that it knows about to ask about the website that you want to visit. Think of these DNS servers as numerous phone books of the internet which are regularly updated. In turn, the DNS server reverts back with a (or often several) IP addresses of the website that you want to reach.
This was a tiny summary describing the task of DNS servers, you can visit Cloudflare’s fantastic blog post on it if interests you.
I won’t delve into the detail as to the structure of DNS requests or the underlying UDP frames that carry these as payload other than stating that the DNS query is encapsulated by a UDP frame and is then catapulted to the realms of the internet in hope of a response from the DNS server (UDP is stateless, connectionless and unreliable).
If you are interested to read up more on the structure of DNS packets you can have a look at this fantastic article titled “UDP Socket Programming: DNS” and if you want to learn more about the structure of UDP frames, you can have a look at the Wikipedia article on UDP.
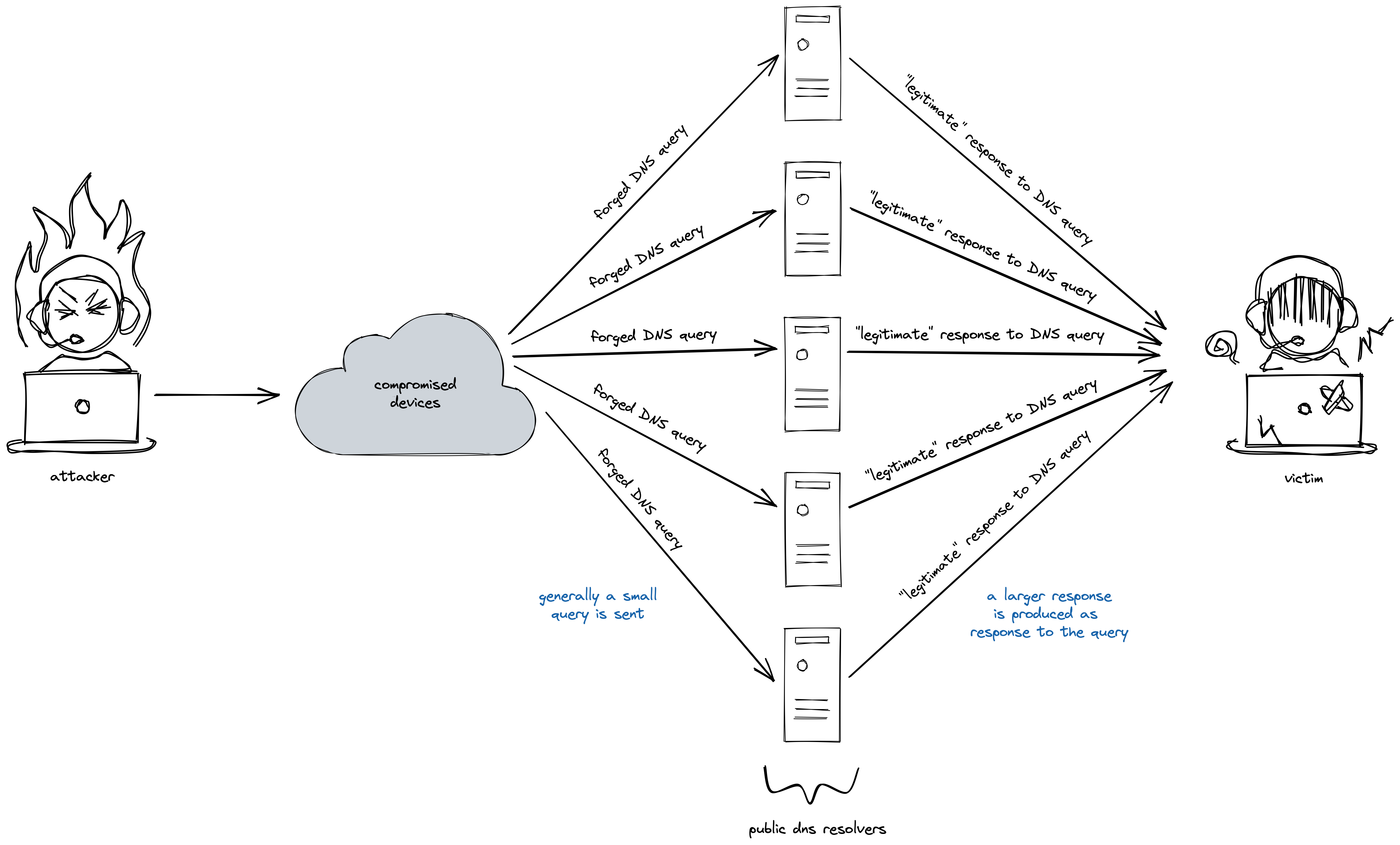
When there is a disparity between the size of the response of a query and the query itself, an attacker is able to exploit the difference and gain more damage from a lesser expense. Responses to a DNS query such as zone transfers or a query for all resource records are generally a lot larger than the query message itself.
If you run dig @1.1 ANY google.com command in your terminal and capture the resulting traffic, you will notice
something like the screenshot below.
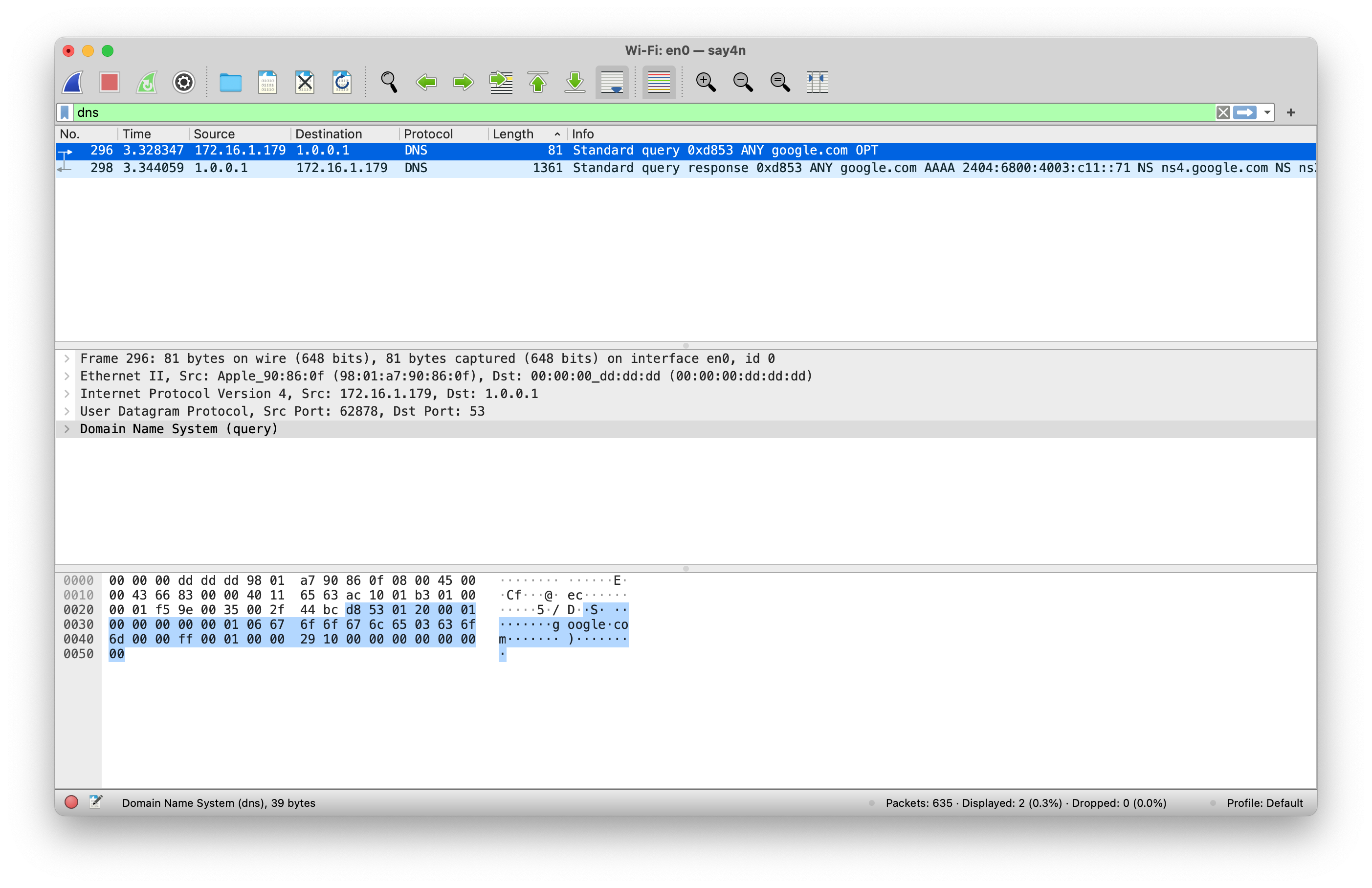
As you can observe from the screenshot, the outgoing request is a mere 81 bytes in length, whereas the incoming response is 1361 bytes in length. That is almost a 17 times request to response ratio!
Now the keen eyed readers amongst you may have noticed the source IP address field from the screenshot of the DNS request above.
What the attacker needs to do is to craft this DNS query in such a way that the source IP address for the query is altered to be the attacker’s victim’s IP address. When this is done, the responding DNS server will mistakenly assume that the the DNS query originated from the victim and sends its response to malicious query to the victim server.
The attackers typically use large botnets to generate such spurious DNS queries and the deluge of responses from various DNS servers causes the victim to become overwhelmed by the sheer bandwidth of traffic that it is ill-prepared to handle.
The captured traffic from a DNS request with an altered source IP will look something like this.
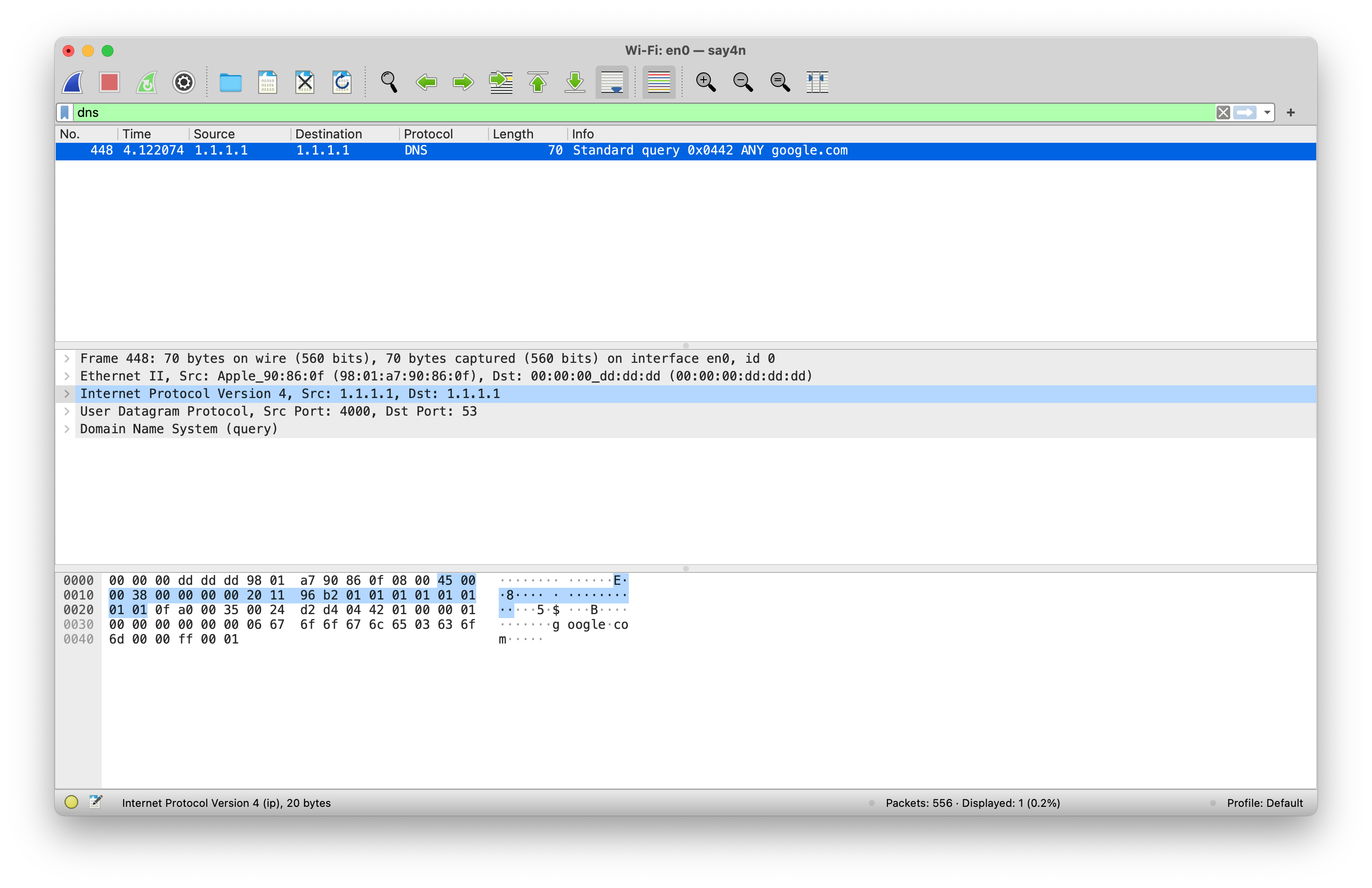
Notice the source and the destination IP address fields are the same in the picture and I can assure you that my IP address is not 1.1.1.1. When the DNS server replies (if it replies at all) to this query, it will be sent to the altered source IP address and not the attacker’s original IP address.
Visit https://github.com/say4n/dns.amplify to have a look at the source code. The readme and the comments in the codebase should be sufficient to navigate around and play with it.
]]>Be sure to check them out!
Head over to Apple’s getting started with metal-cpp guide and follow the
instruction in the section titled “Step 1. Prepare your Mac”.
Additionally, make sure to also follow the part of the instruction that describe how to use metal-cpp as a single
header include (section titled “Metal-cpp single header alternative”) in a project.
We will be using Xcode for development, I used version 13.2.1 (13C100).
At this stage, this post assumes that you have the metal-cpp sources extracted to a convenient location and that you
have executed the command to use metal-cpp as a single header include by following the steps described previously.
The next step is to set up an Xcode C++ project.
Create a new project with the command line application template in Xcode with macOS as the target platform.
Make sure to select C++ as the language!
metal-cppIn the build settings tab under the project navigator, search for the “Header Search Path” and set it to the base directory where you extracted metal-cpp.
Next search for “C++ Language Dialect” and set it to C++17 or higher.
And that’s it, we are now ready to use the metal-cpp to interface with Apple’s Metal API in our C++ project.
Our tiny metal program will perform the very basic operation of multiplication. To that end, here is the code that defines the operation in the metal shading language.
//
// compute.metal
// metal-test
//
// Created by Sayan on 28/12/21.
//
#include <metal_stdlib>
using namespace metal;
kernel void work_on_arrays(device const float* inA,
device const float* inB,
device float* result,
uint index [[thread_position_in_grid]])
{
result[index] = inA[index] * inB[index];
}
What this does is it takes array elements from two float array inA and inB and stores their product in a third array result.
You can read up more about the metal shading language in its language specification here.
You can also follow Apple’s Swift/Objective-C tutorial for performing calculations on a GPU for a better introduction to programs in the metal shading language.
Now that we have defined our compute operation, we need to write the driver code that actually makes it all happen! The files of interest and their respective functions are described in the following sections.
This is the main file that ties everything together.
It instantiates an NS::AutoreleasePool and a MTL::Device object.
It then instantiates an object of the compute wrapper class that we describe below.
Then it passes the Metal device to be used for compute to the said wrapper class.
The data for the compute operation is then prepared and the compute command is send.
Finally, the NS::AutoreleasePool is released.
This defines the metalComputeWrapper class, a wrapper class that takes a MTL::Device and performs operations define by the kernel in metal shading language.
It also prepares the various buffers as well as the data required by the various operations defined in the compute kernel.
It also verifies that the results produced after computation are as expected and lie within a margin of error.
This file contains the implementations of the various member functions of the metalComputeWrapper class.
Note: This blog post is a Work in Progress and content may be added to it from time to time.
]]>The law of iterated expectation or the law of total expectation states that
\[E[X] = E[E[X \mid Y]]\]or, in other words the expected value of the conditional expected value \(X\) given \(Y\) is the same as expected value of \(X\).
Well, the LIE is used in the derivation of the Bellman equations of reinforcement learning, let me show you how. From the definition of the value function (expected value of the discounted return), we have
\[\begin{aligned} V^\pi (x) & = E_\pi \left[\sum_{t=0}^{\infty} {\gamma ^ t r(x_t, a_t) \mid x_0 = x} \right]\\ & = r(x, \pi(x)) + E_\pi \left[ \sum_{t=1}^{\infty} {\gamma ^ t r(x_t, a_t) \mid x_0 = x} \right]\\ & = r(x, \pi(x)) + \gamma E_y \left[ E_\pi \left[ \sum_{t=1}^{\infty} {\gamma ^ {t - 1} r(x_t, a_t) \mid x_0 = x, x_1 = y} \right] \right] \quad \color{CornflowerBlue}{\text{(LIE used here)}}\\ & = r(x, \pi(x)) + \gamma \sum_y {P(y \mid x, \pi (x))} E_\pi \left[ \sum_{t=1}^{\infty} {\gamma ^ {t - 1} r(x_t, a_t) \mid x_1 = y} \right] \quad \color{CornflowerBlue}{\text{(by Markov property)}}\\ & = r(x, \pi(x)) + \gamma \sum_y {P(y \mid x, \pi (x))} V^\pi (y) \qquad \blacksquare \end{aligned}\]These are the Bellman equations for the value function!
]]>